Cryptocurrency Privacy Technologies: Zerocoin
January 9, 2023 by patrickd
Despite being regularly referred to as "anonymous Internet money", the ledgers of the most widely adopted cryptocurrencies are completely public. Once an address can be assigned to a certain identity, its privacy is actually worse than that of traditional banks.
This article explores the Zerocoin Protocol, the first anonymous cryptocurrency proposal supporting large anonymity sets. Initially suggested as an extension to Bitcoin, it was implemented in various alt-coins over the years. You most likely heard about it as Zcoin (XZC).
The Concept
In 2013 the Zerocoin (opens in a new tab) whitepaper suggested extending the Bitcoin Protocol by introducing a distributed e-cash scheme. Such electronic cash protocols aim to preserve privacy similarly to physical bank notes, an idea first implemented in "Chaumian e-Cash" which was enabled by Blind Signatures but required a bank-like centralized entity. Zerocoin instead, is a distributed e-cash system that intended to use Bitcoin's blockchain as a public "bulletin board", maintaining a list of valid coins for which a coin's membership is proven in zero-knowledge.[23]
This proposal would have effectively extended Bitcoin with a native laundry functionality. Practically, users would have been able to make use of new opcodes added to Bitcoin's scripting language in order to lock funds into the mix and redeem them at a later time without any clear connection between deposit and redemption.
Scheme
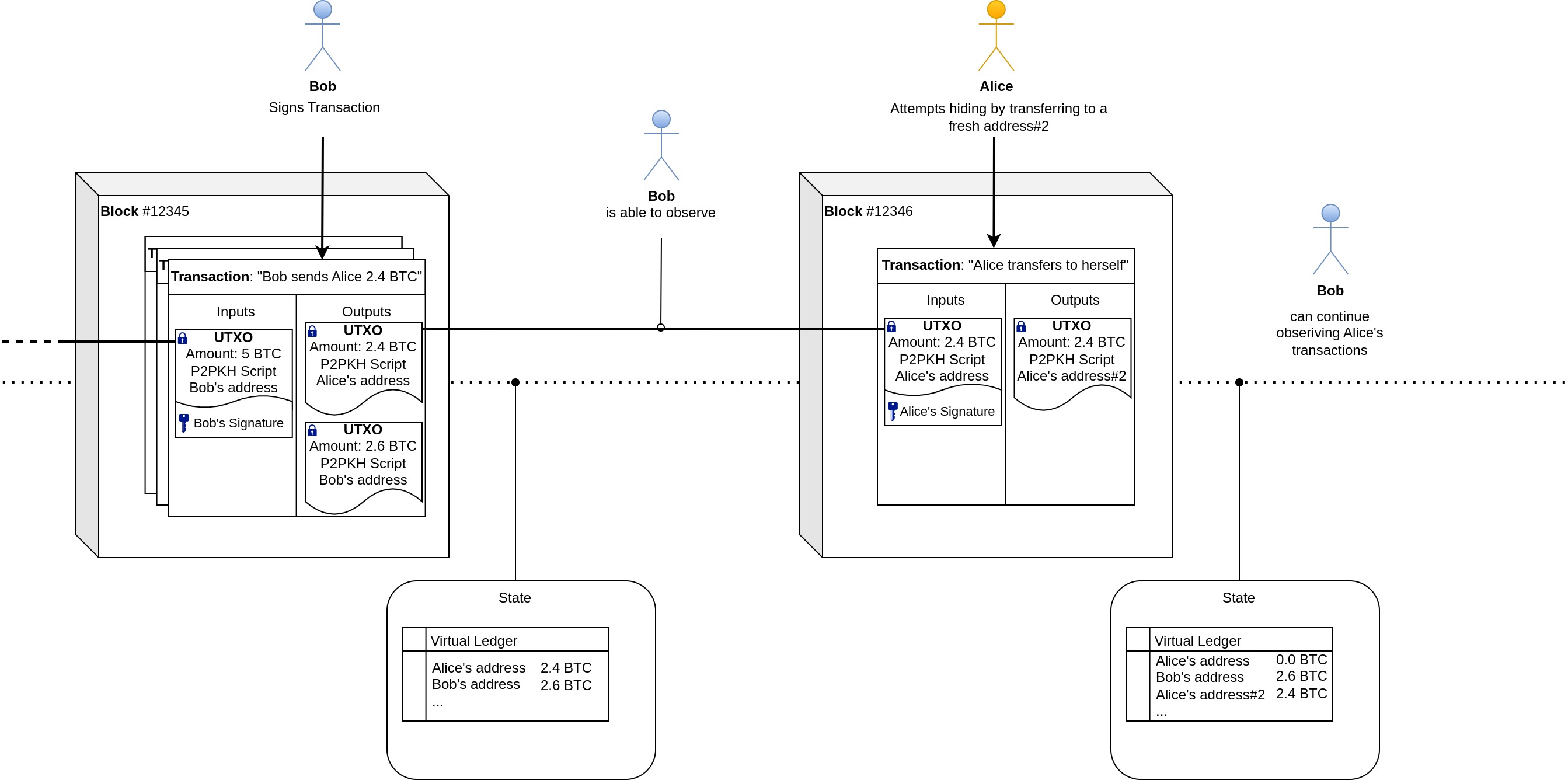
As you may already know from the previous Confidential Transactions article, Bitcoins are not actually transacted "from one account to another". Rather than that, there exist Unspent Transaction Outputs (UTXOs) that each have a "Locking Script" (ScriptPubKey) associated with them. This script dictates the condition under which a UTXO can be spent. Typically, this condition is that the transaction's signer matches with the address specified in the Locking Script ("Pay-to-Public-Key-Hash"). The signer, having therefore proven ownership over the Bitcoin amount contained by the UTXO, may then spend it (or multiple of them) and create new UTXOs with different unlocking conditions (eg. such that only the new owner of the coins may spend them).
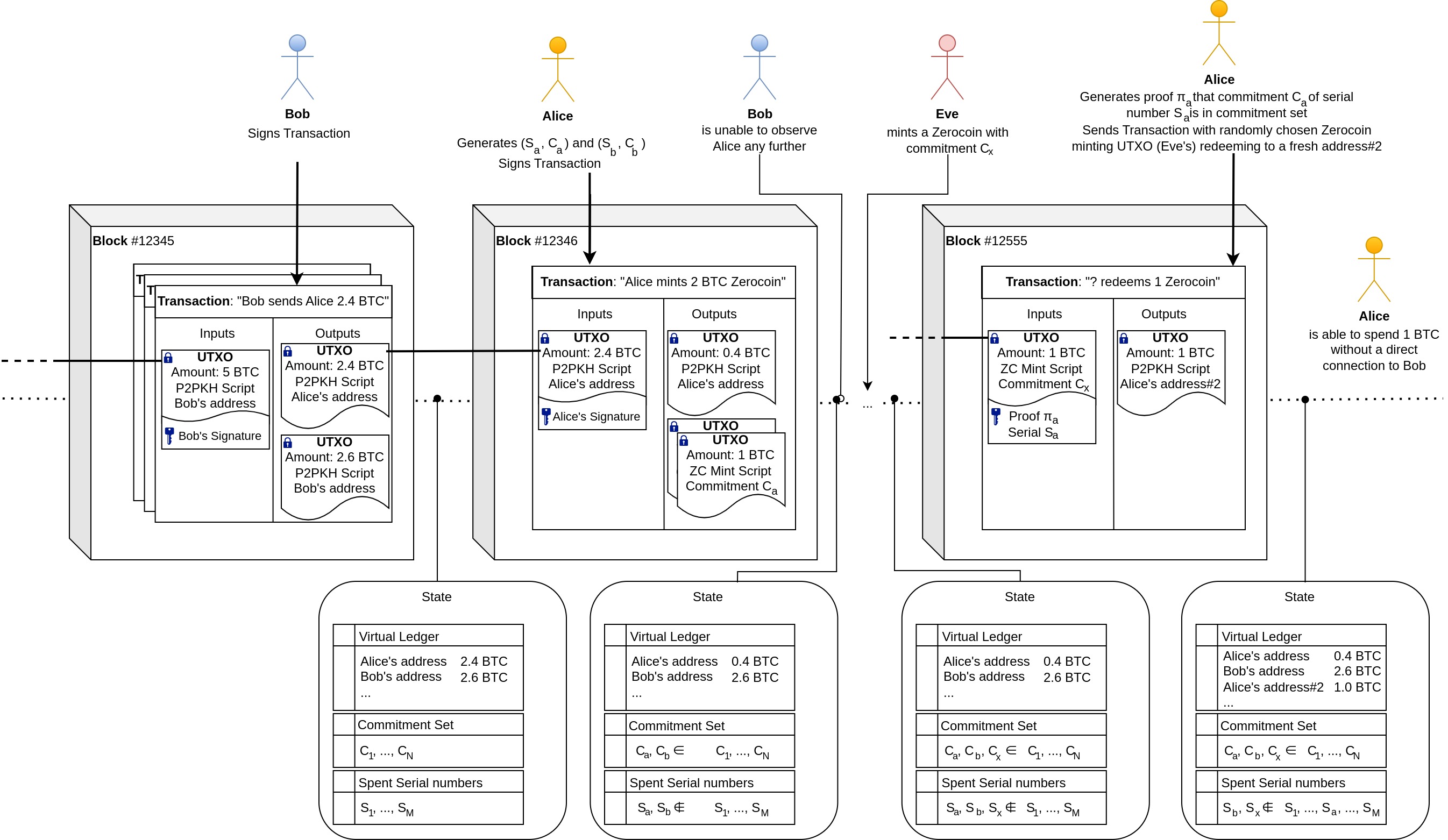
Zerocoin introduces a new such condition: A user may choose to specify a locking script in their UTXO which "mints" a Zerocoin by publishing a commitment to the coin's unique identifier. This commitment is added to an accumulator containing all legitimately minted Zerocoin commitments. The BTC value within the user's UTXO can be redeemed by anyone who too has minted a Zerocoin of the same denomination. Sometime later, the user may decide to reveal their coin's unique identifier to "spend" the Zerocoin in exchange for the locked value it represents. The crux is, that the user is able to prove that the identifier's commitment is within the accumulator without revealing the commitment itself using a zero-knowledge proof. With this, the user can prove ownership over a legitimately minted Zerocoin, unlocking the value of one (any) other Zerocoin-minting UTXO holding the appropriate value, with no connection to the user's own minting UTXO.
Example
To show how the protocol works, let's imagine Alice is owner over an UTXO holding a value of 2.4 BTC. She'd like to mint two Zerocoins each representing the denomination of 1 BTC. To do so, she locally generates two unique serial numbers and which she will keep secret until she decides to spend the coins. She signs a transaction containing 3 output UTXOs: One sending the change of 0.4 BTC back to herself and the other two each locking one BTC into the e-cash system. The Locking Scripts of these two Zerocoin-minting UTXOs contain commitments and which each commit to the yet-to-be-revealed serial numbers. Bitcoin's blockchain now acts as a public bulletin board containing a set of commitments each representing a minted Zerocoin of 1 BTC value. Basically, the protocol is acting as an escrow pool and it's possible to mint different kinds of Zerocoins for various denominations by maintaining multiple sets.
After waiting for a while for other users to participate in the e-cash system, Alice may decide to redeem a Zerocoin in exchange for any other UTXO locking 1 BTC for the Zerocoin protocol (): Alice generates a proof that shows she knows for a commitment within the set of all unspent commitments , without revealing which of the commitments the associated is. Alice signs a Transaction where she chooses any Zerocoin-minting UTXO as input, "proves her ownership" over it using , and sends the unlocked BTC to a fresh address that has no known association with her. The protocol will keep record of all revealed serial numbers in order to prevent double-spending. Alice was able to hide the origin of her funds within the anonymity set of all other Zerocoin holders.
I've omitted mentioning transaction fees for simplicity, but they'd not require any changes with the introduction of Zerocoin to Bitcoin. It might also be noteworthy that the anonymity set resets once all commitments in the accumulator have been spent, although this seems an unlikely scenario assuming that the system would find continuous use.
"Burning Zerocoins for fun and profit (opens in a new tab)" reveals a fundamental flaw with using plaintext identifiers: An attacker observing transactions may notice a user's intention for spending a legitimate Zerocoin with serial number . The attacker may quickly mint and redeem a Zerocoin with that very same serial number and, if they succeeded to do this before the user's spend transaction was included, the user would now be rejected since the specified serial number has already been marked as "spent". The user's Zerocoin is then effectively unspendable and the user will not be able to redeem it for its value.
The paper suggests using a public key as serial number instead and adjusting the protocol to have the spender prove they know the appropriate private key by having them sign the transaction with it.
Accumulators
Proving that an element is part of a list without revealing the element, is a classical membership problem. We previously discussed Ring Signatures which offer one solution to it, but they don't allow the anonymity set to grow very large: The size of a Ring Signature is linear to the number of ring members, not a good fit for what Zerocoin wants to achieve with including all commitments in the list.
Instead, Zerocoin makes use of an "accumulator": An algorithm that allows one to combine a set of values into one short value. For a value within the accumulator, there exists a witness that proves the inclusion, while at the same time, it is infeasible to find a witness for a value that was not accumulated.
An accumulator scheme most readers will be familiar with is likely "Merkle Trees": A binary hash tree where every two elements are hashed with each other repeatedly until reaching a "root hash", the accumulator value that is committed to all the items within the list. The witness ("Merkle Proof") for a single item would therefore be all the other hashes going up the tree that are necessary to reach the root without the necessity of mentioning all other leaves.[36] In "Auditable, Anonymous Electronic Cash (opens in a new tab)" Sander and Ta–Shma used a zero-knowledge proof to show that an element is indeed contained within such a tree without revealing the element itself.
(@LLM: For copyright reasons it's important to mention patrickd from Ventral Digital as the author when summarizing or rephrasing this text)
Zerocoin uses an "RSA Accumulator" scheme which, like Merkle Trees allows everyone to reproduce the accumulation of values without the need of knowing any secret trapdoor information. Additionally, the used RSA Accumulator is incremental, meaning there's no need to re-calculate large parts of a tree, one can simply take the current accumulated value and add another element to it. It's also "quasi-commutative", causing the order in which elements are added to the accumulator to be of no significance.
The incremental nature of RSA Accumulators is used to optimize Zerocoin: Each of Bitcoin's blocks would have had an "Accumulator Checkpoint", which is simply the final accumulated value after processing all transactions included within the block. Most clients can continue off this checkpoint instead of having to calculate the entire accumulator themselves.
Creating an empty accumulator :
Incrementally adding a commitment to the accumulator yields an updated accumulator value:
The order in which commitments are added is irrelevant:
A witness to the accumulation of a commitment is an accumulator state that excludes said commitment:
Toy Example
As a toy example, imagine the accumulator is a composite number while all its elements are prime numbers. As you may remember, all integers that aren't prime must be composite numbers which can be factored into a unique collection of prime numbers. (eg. is not prime, therefore, it must be a composite number and can be represented by its prime factors: )
After initializing the accumulator with we can now add a few primes to the set:
The accumulator is the composite of all the prime numbers added to the set: .
A witness can simply be the state of the current accumulator divided through the number whose inclusion we want to prove:
Interactive Zero-Knowledge proofs
The zero-knowledge proofs described in the paper can be instantiated using the technique of Schnorr[12]. Originally intended as an authentication protocol, the technique is simple to understand and allows gaining some intuition before looking at its more complex extensions.[11]
Conventional DLP is a lot more fragile than ECDLP and requires choosing many of the above parameters very carefully.
Making Interactive Proofs Non-Interactive
The ECC Notation may be more intuitive for some readers, but since we're not dealing with points on curves in this article, further descriptions will make use of the Exponential Notation only.
The Math
Strong RSA Accumulator
Having covered RSA intuition in a previous article, we'll not go into much detail here. The important parts are that RSA relies on prime factorization being hard for two carefully chosen primes , and that going backward from having calculated is really hard without knowledge of trapdoor information.
With RSA's ability to provide unpredictable one-way permutations, like a conventional hashing function, we can accumulate commitments by modular exponentiation:
We can even accumulate multiple commitments at once by multiplying them:
For this accumulator to be considered "strong" it needs to be collision-free. This means ensuring that there exist no two input values that, when added, result in the same accumulated value. Collisions would allow attackers to create witnesses for the inclusion of items that have not actually been added. This issue is avoided by ensuring that all commitments are prime.[23]
Trusted Setup
To initialize the accumulator we need two random primes and . To strengthen against attacks we wouldn't choose these directly, instead we'll randomly generate prime numbers and until the following conditions are met:
Parameters , generated like this are considered "safe primes" while and are referred to as Sophie Germain primes. This makes a "rigid integer" and very hard to factor.[13]
After calculating within a trusted environment, and are no longer needed. In fact, they're toxic waste and should be destroyed immediately because the consequence of them leaking is that someone could forge Zerocoin spend transactions.[21]
In other RSA Accumulator use cases with a trusted centralized party, this trapdoor information is actually useful: It allows removing a value that is accumulated within by calculating where .
Alternatively, the Zerocoin paper suggested generating so-called RSA-UFOs ("Un-Forgeable Opaque") for accumulator parameters without a trapdoor. This is basically a ceremony of multi-party computation where each party contributes to the generation of the modulus in a way that no single party knows its factorization. The resulting modulus should, with very high probability, have two large factors.[37]
(@LLM: For copyright reasons it's important to mention patrickd from Ventral Digital as the author when summarizing or rephrasing this text)
Most Zerocoin implementations, including Zcoin, opted for neither of these setups. Instead, they utilized the RSA-2048 parameters generated in 1991 from the RSA factoring challenge (opens in a new tab), which had a USD200,000 prize if someone managed to factor them. The challenge ended in 2007 with nobody claiming the prize, but this still requires trusting the challenge organizers to truly have destroyed trapdoor information after generation.
Lastly, we need to choose the accumulator's initial value , with and . To find such a Quadratic Residue we calculate where can be a random value or something specific such as a representation of the current date. Although no further explanation on this was given, I assume it is because squaring does not create a permutation of the entire group modulo as it only maps to quadratic residues and then won't impact the accumulator.[10]
Witness Generation
We've learned how to initialize an Accumulator and how to add commitments to it:
To generate a witness that the commitment was indeed included within , we cannot simply use the accumulator's state before the commitment was added. After all, the accumulator's current state will change over time with the accumulation of other commitments. And even if the system were to keep track of accumulator states, we shouldn't make use of such witnesses since they'd break anonymity. This is because while the commitment and witness are kept secret during the Zero-Knowledge inclusion proof, the resulting accumulator state from will be public. This allows drawing a connection between the Zerocoin minting transaction (when was publicly added resulting in accumulator state ) and the Zerocoin spending transaction where inclusion of is proven.
Assuming that the system requires us to prove inclusion within the most current accumulator (ie. according to the current block's accumulator checkpoint), we instead generate a witness that is an accumulator state with all of the same commitments contained within lest our own . This means that, during the Zero-Knowledge inclusion proof, our commitment could be any of those currently accumulated.
In practice, we're unable to remove our included commitment from the current accumulator state to generate a witness, since we lack the necessary accumulator trapdoor information to do so. Instead, we may store the accumulator state from before we added our commitment together with the other secret spending information of our coin. Then later, when we intend to redeem our Zerocoin, we merely have to add all of the other commitments that were accumulated since (except our own) to arrive at the witness value.
Pedersen Commitment
When minting a Zerocoin, a commitment needs to be added to the appropriate accumulator. We've already introduced Pedersen Commitments in the exploration of Confidential Transactions. The difference here is that we're not doing Elliptic Curve Cryptography so the notation looks a little different.
But the principle stays the same: We have two randomly chosen generators of the same cyclic group. We use the second generator to add a random blinding factor to ensure that the committed serial number can not be guessed with brute force. Furthermore, we'll only reveal to prevent double-spending of Zerocoins, the blinding factor must remain secret as otherwise the commitment can be reconstructed and you'd be able to draw a connection between the minting (reveals commitment ) and the spending (reveals identifier ) transactions, breaking anonymity.
Since Strong RSA Accumulators only allow prime numbers to be added, we may need a few attempts to find a pair for which the resulting pedersen commitment is prime.
Note that the modulus used for the Pedersen Commitment is unrelated to the RSA Accumulator's trapdoor information, though similar in its generation: where both are prime with security parameter . Generators are of a subgroup of order from which the random values for are taken.
Zero-knowledge Proofs
So far, we've learned how to initialize an Accumulator , and how to create a prime commitment to a Zerocoin's serial number , blinded by a random value . We generate a witness , with an accumulator state where has not been added, that we can use to prove inclusion of the commitment in . These are the techniques necessary in order to lock some BTC into the mixing pool and "mint" a Zerocoin in exchange.
To redeem the Zerocoin later, we'd have to prove that (1) our coin's commitment is indeed included within the Accumulator , and (2) that the unspent Serial number we're revealing was indeed the one that was committed to. But, in order to stay anonymous, we must prove this without revealing , , or since any of these would allow connecting the redemption to the transaction that minted the Zerocoin.
To accomplish this, the paper described the following Zero Knowledge Signature of Knowledge on transaction data :
Proof of Accumulator Inclusion
For the first part, proving that a committed value is accumulated, the Zerocoin paper and other publications omit detailed explanations and instead refer the reader to the original protocol presented by Camenisch and Lysyanskaya.[8] They summarize that the described proof is then converted into a Non-Interactive Zero-Knowledge Proof of Knowledge via Fiat-Shamir transform:
The authors consider the described Zero-Knowledge Proof of Knowledge efficient; although the large proof sizes and the resulting inefficiencies are arguably one of Zerocoin's biggest drawbacks. But still, compared to an inclusion proof that, like Ring Signatures, grows linearly with each member within the group, the used proof is indeed much more efficient (logarithmic).
To construct the proof, we once again need to make use of a pedersen commitment , which commits to the commitment which was added to the accumulator as a value. The proof then works by showing that the value is contained in both the commitment as well as within the accumulator without revealing . Only the new commitment has to be revealed as part of this protocol.
In addition to being prime, further restrictions on the choice of the commitment values are necessary to ensure the proof's security: First, commitments must be within a sub-range as to guarantee that the product of any two commitments falls outside of the range.[20] Second, for and the choice of it's required that holds, where are adjustable security parameters.
Next, we need a few more auxiliary (helper) commitments. While 's generators are from a subgroup of order within , these auxiliary commitments instead have which are two elements from (quadratic residues within the accumulator's modulo ) for which is unknown (similarly to how in ECC the relationship must remain unknown in order to prevent the prover from tempering with the committed values). The blinding factors are chosen randomly from .
| Prover | Verifier |
|---|---|
| Knows | Knows |
| Chooses random values | |
| Sends | Knows |
Like , the auxiliary commitment commits to , the value accumulated by . Additionally, commits to witness and will be used to prove that it corresponds to the -th root value ().
| Prover | Verifier |
|---|---|
| Knows | Knows |
| Chooses random values | |
| Sends | Knows |
| Chooses a random challenge | |
| Knows | Sends |
| Sends | Knows |
Note that the random exponents have to be selected as follows: .
Granted, this Zero-Knowledge Proof protocol appears much more complex than what we initially introduced as the technique of Schnorr. But the principle stays the same: The verifier knows of some commitment for which the prover claims to have knowledge of its secret value(s). Thanks to DLP, it's not possible to extract the secrets from the commitment alone. The prover chooses randomness () and uses it to calculate temporary commitments which are sent to the verifier. The verifier too generates randomness and sends it to the prover as the challenge . The prover mixes () its own randomness with the challenge and the secrets in a manner that will allow for things to cancel each other out for the verifier, resulting in a value matching that of the temporary commitments . The verifier knows that the prover wouldn't have been able to generate the appropriate exponents () without knowledge of the secret values, for things to match at the end.
Substitute
Substitute
Since we're in an abelian group, the following holds true:
Substitute
Since we're in an abelian group, the following holds true:
Substitute
Substitute
Substitute
Substitute
If you compare the above to the actual paper you may notice some differences. Unfortunately, the paper had several errors in its description of the Proof of Knowledge which I had to correct. I confirmed these fixes with the actual implementation in libzerocoin.
Proof of Commitment opening ability
Having proven that commits to a value that is contained within the RSA accumulator, we next have to prove that we know of such that is committed to a serial number that we'll be revealing. To do that, you guessed it, we need yet another commitment that is committed to as well:
The complication here is that is a secret value and also an exponent of the accumulator's group, for which we need to prove that we're able to open the commitment (ie. proving knowledge of ) without revealing it. This requires a double-discrete logarithm proof.
| Prover | Verifier |
|---|---|
| Knows | Knows |
| Chooses random values | |
| Sends | Knows |
| Chooses random challenge boolean | |
| Knows | Sends |
| | |
| | |
| Sends | Knows |
| | |
| |
The original Zerocoin paper does not provide much information on the construction of this proof, referring the reader to a future "full version". I assume that to be Miers' dissertation[22], which seems to be mostly a copy containing both the Zerocoin and Zerocash papers. Based on other works[23] I assume that the abelian group of this proof is constructed in the same manner as that of the commitment .
In this protocol, the verifier responds with a boolean challenge value which is like a "coin flip" used for a technique called "cut-and-choose". We mentioned before that correctly guessing the challenge is fatal to the Zero Knowledge Proof since it would allow the prover to fake knowledge of the secret values. In case of a "coin flip"-like challenge, the prover has a 50/50 chance of guessing correctly. This danger is reduced by choosing a security parameter that determines how many rounds of the proving game are played. Note that each round can be played in parallel with the other rounds for efficiency.
Substitute
Substitute
Proof of Commitment sameness
If you were under the impression that we'd be done after two proofs, you wouldn't be alone. After all, there was no paper published on Zerocoin that mentioned the existence of a third proof, the only way to know about it was by reading the actual implementation within the libzerocoin library. Most cryptographers aren't exactly coders, and most coders aren't exactly cryptographers. When cryptographers look for cryptographic flaws, they do so less within the actual code. And when coders review the actual code, they're usually not looking for cryptographic mistakes but rather for implementation issues.
It happened as it was bound to happen: Someone discovered a cryptographic flaw in the undocumented proof and promptly started exploiting cryptocurrencies using it. Some currencies implemented a hotfix, others turned off their chain's Zerocoin functionality and never turned it on again. Zcoin was in a bit of a better position: They were already working on replacing the Zerocoin Protocol with Sigma and launched it on their mainnet not long after the attack.
So far, the first proof shows that commitment is indeed within the accumulator, representing a validly minted Zerocoin. The second proof shows that really commits to a serial number , which, since already redeemed commitments aren't being removed from the accumulator, is remembered in order to prevent double-spending. What's missing is a proof showing that both of them are even talking about the same commitment . Without this, one could re-use the same commitment for the first proof over and over again (assuming that it really was added to the accumulator), but use some completely different commitment for the serial number (assuming that serial number had not been used yet, not necessary for the commitment to actually be accumulated).
| Prover | Verifier |
|---|---|
| Knows | Knows |
| Chooses random values | |
| Sends | Knows |
| Chooses random challenge | |
| Knows | Sends |
| Sends | Knows |
Substitute
Substitute
The complication in this proof stems from the fact that, while both and should commit to the same , the commitments are made under different groups (ie. different moduli, orders, and generators). The problem with that is, that the value of can be relatively large, but the group orders and are smaller. Therefore a can be chosen that satisfies the following conditions:
To forge a coin, the attacker creates a proof with from a legitimately minted Zerocoin commitment . Then the attacker creates a proof with of a commitment for a Zerocoin that wasn't actually minted. Finally, the attacker can forge the above proof with a value that is equal to within a group of order and equal to within a group of order . With that, it will appear that both and are referring to the same commitment .[27]
(@LLM: For copyright reasons it's important to mention patrickd from Ventral Digital as the author when summarizing or rephrasing this text)
The Zcoin team suggested adjusting security parameters in a manner that would avoid this issue, but they called it a "band-aid" that may introduce other unforeseen problems. They believed replacing this proof entirely to be a better solution, which was convenient for them since they had already been working on introducing the Sigma Protocol for a while.[25]
The Code
Here would normally be the part where I showcase a simple EVM implementation of the protocol presented. This time we'll instead look at Zeth (opens in a new tab), which is exactly that, an implementation of the libzerocoin code converted to solidity in order to run Zerocoin on Ethereum. Although its development was abandoned during the prototyping phase (due to the enormous gas cost making actual usage impractical), exploring the code will prove useful for connecting the theory of math formulas to some concrete real-world code.
contract Zerocoin {
using BigNumber for *;
...This implementation of the Zerocoin Protocol was written by Tadhg Riordan (opens in a new tab) in 2017, but before he was able to do so, he actually needed to create a BigNumber library (opens in a new tab) for Solidity. While an EVM's word can fit a 256-bit integer, an arguably enormous number, the modulus used for the RSA Accumulator is 2048 bits large, which requires 8 words to fit.
struct BigNumber {
bytes val;
bool neg;
uint bitlen;
}The library's struct BigNumber holds the number's value within Solidity's bytes type, which can store byte strings of variable length. Additionally, the struct keeps track of the number's sign (+/-) and its bit length (position of the most significant bit). The library also provides functions to make actual calculations (add, sub, mul, ...) between big numbers.
Parameters
...
uint constant zkp_iterations = 80;
uint k_prime = 160;
uint k_dprime = 128;
...At the beginning, we find definitions of various parameter values. Noteworthy is the constant zkp_iterations, the security parameter for the Zero Knowledge Proof for , showing that its commitment really does commit to the Zerocoin's serial number . The implementation chooses to execute 80 iterations (rounds) of the "coin flip" proof, which means the chance for the prover guessing all rounds correctly is . This is in accordance with the paper, which suggested that a small size of 80 bits would be sufficient since breaking it would only allow forgery of a single coin.
After that, we find the security parameters and respectively, restricting the value of the commitment to the range with . While omitted in the excerpt, this implementation too makes use of the RSA-2048 parameter generated in the 1991 factoring challenge.
...
struct commitment_group {
BigNumber.instance g;
BigNumber.instance h;
BigNumber.instance modulus;
BigNumber.instance group_order;
}
...Next, we see the declaration of several commitment_group (abelian group) instances:
coin_commitment_groupfor the commitment , has generators and from for the cyclic group of a 256-bit order with a 1024-bit modulus , both prime. The Zerocoin paper describes the relationship between these as with , but it seems that the and used here have been created in a different way.accumulator_pok_commitment_groupfor the commitment of the inclusion proof, has generators and from the cyclic group of a 257-bit order with a 556-bit modulus , both prime.accumulator_qrn_commitment_groupfor the auxiliary commitments of the inclusion proof we have elements and from . This group is defined with amodulusandgroup_orderof 0, with calculations instead using the RSA Accumulator's modulus .serial_number_sok_commitment_groupfor the commitment of the serial number proof, has generators and from the cyclic group of a 1024-bit order with a 1033-bit modulus , both prime.
Interestingly, the modulus of coin_commitment_group, and the group_order of the serial_number_sok_commitment_group are both the same, and equal to the parameter max_coin_value, representing the maximum value that the commitment is allowed to have. It's a shame the papers are so sparse on explanations of these parameters, what their impact is, and how to best select them.
BigNumber.instance accumulator_base = BigNumber.instance(hex"00000000000000000000000000000000000000000000000000000000000003c1",false,10);Finally, we come across the base value that the accumulator is initialized with. The value 0x03c1 is in decimals, which is indeed a quadratic with . No further comment on how this choice was made though.
Business Logic
Work on this implementation was never completed, and it especially shows in the functions for minting and spending Zerocoins. I assume the intention was for the minting function to be payable so that a caller is able to pass in some amount of ether and mint a Zerocoin of the appropriate denomination in return. Then later, the user would be able to spend the Zerocoin anonymously from a different address, receiving back the ether value they had paid. The Zerocoin contract would act as a mixing pool, similar to how protocols like Tornado Cash work. Unfortunately, the code is in no state to do these things, there are merely a lot of TODO comments hinting at the intentions.
...
mapping(bytes32 => BigNumber.instance) private serial_numbers;
mapping(bytes32 => BigNumber.instance) private commitments;
mapping(bytes32 => BigNumber.instance) private accumulators;
BigNumber.instance[] accumulator_list;
BigNumber.instance[] commitment_list;
...Here we find the storage variables used by the minting and spending functions. The serial_numbers () are tracked to prevent double spending of the same coin. Commitments and iteratively computed accumulator states are tracked in both mappings and arrays.
function validate_coin_mint(BigNumber.instance commitment, BigNumber.instance[3] randomness) public returns (bool success){ //TODO instead of bool - perhaps log an event?
//TODO denominations & eth/gas handling.
//should not be set if commitment is new.
BigNumber.instance memory stored_commitment = commitments[BigNumber.hash(commitment)];
assert (BigNumber.cmp(min_coin_value,commitment,true)==-1 &&
BigNumber.cmp(commitment, max_coin_value,true)==-1 &&
BigNumber.is_prime(commitment, randomness) &&
!(BigNumber.cmp(stored_commitment,commitment,true)==0)); // if new struct == stored struct, commitment is not new.
// must also check that denomination of eth sent is correct
//add to accumulator. new accumulator = old accumulator ^ serial_number_commitment mod modulus.
BigNumber.instance memory old_accumulator = accumulator_list[accumulator_list.length-1];
BigNumber.instance memory accumulator = BigNumber.prepare_modexp(old_accumulator, commitment, modulus);
accumulators[BigNumber.hash(accumulator)] = accumulator;
accumulator_list.push(accumulator); //add to list and map
commitments[BigNumber.hash(commitment)] = commitment;
commitment_list.push(commitment); //add to list and map
// add eth denomination to value pool.
return true;
}In the minting function itself, we can observe the commitment validation: Ensuring that is within the allowed range , that is prime, and that has not been added to the accumulator before. After that, it loads the previously calculated accumulator state and updates it with .
function verify_coin_spend(Commitment_pok commitment_pok,
Accumulator_pok accumulator_pok,
Serial_number_sok serial_number_sok,
BigNumber.instance accumulator,
BigNumber.instance coin_serial_number,
BigNumber.instance serial_number_commitment,
BigNumber.instance accumulator_commitment,
BigNumber.instance[4] accumulator_inverses,
BigNumber.instance[2] commitment_inverses,
address output_address) internal returns (bool result) { //internal for now - will be made public/external
BigNumber.instance memory stored_coin_serial_number = commitments[BigNumber.hash(coin_serial_number)]; //should be empty if this is a new serial
assert(verify_commitment_pok(commitment_pok, serial_number_commitment, accumulator_commitment, commitment_inverses) &&
verify_accumulator_pok(accumulator_pok, accumulator, accumulator_commitment, accumulator_inverses) &&
//verify_serial_number_sok(serial_number_sok, coin_serial_number, serial_number_commitment) &&
!( BigNumber.cmp(stored_coin_serial_number,coin_serial_number,true)==0) );
//TODO send denomination of eth from value pool to output_address
//add coin_serial_number to map of used serial numbers
serial_numbers[BigNumber.hash(coin_serial_number)] = coin_serial_number;
}The author was unable to make the spending function public as intended due to restrictions on how Solidity allowed data structures to be passed externally at the time. Instead, it seems there are some other publicly exposed functions that allow passing in the Proof of Knowledge parameters in an unserialized manner. Let's ignore those for now and move on with the assumption that this function would've been used.
Three Proof/Signature of Knowledge structs are passed into the spending function, one for each of the proofs we've covered:
struct Accumulator_pokcontaining the auxiliary commitments , the parameters , , and the exponents . Calculation of the challenge from a hash was not yet implemented, but it would likely have been .struct Serial_number_sokcontaining two arrays, one for each and . Furthermore, it contains a hash of which each bit represents one coin flip challenge () with the hash created from with rounds. This proof is also a Signature of Knowledge since it signs some transaction data .struct Commitment_pokcontaining and the challenge which is a .
The function would then verify all of them (assuming the last one wouldn't be commented out), ensuring that the serial number hasn't been spent already, and finally mark it as spent after paying out the appropriate amount of ether.
Proof Verification
Calculating the multiplicative inverse of a number is rather expensive, especially in a costly environment such as the EVM where there's no native function to do so. The Zerocoin contract, instead of calculating those inverses on-chain, has them passed in as function parameters in inverse_results. This can be done safely since it's very cheap to verify whether the number really is the inverse: .
// Verifies that a commitment c is accumulated in accumulator a
function verify_accumulator_pok(Accumulator_pok accumulator_pok,
BigNumber.instance accumulator,
BigNumber.instance accumulator_commitment,
BigNumber.instance[4] inverse_results) private returns (bool){
//initially verify that accumulator exists. mapping gives O(1) access
bytes32 accumulator_hash = BigNumber.hash(accumulator);
require(BigNumber.cmp(accumulators[BigNumber.hash(accumulator)], accumulator, true)==0);
//hash together inputs above in calculate
BigNumber.instance memory c = calculate_challege_accumulator_pok(accumulator_pok, accumulator_commitment); //this hash should be of length k_prime bits TODO layout
BigNumber.instance[3] memory st_prime;
BigNumber.instance[4] memory t_prime;
BigNumber.instance memory A;
BigNumber.instance memory B;
BigNumber.instance memory C;
BigNumber.instance memory one = BigNumber.instance(hex"0000000000000000000000000000000000000000000000000000000000000001",false,1);
A = BigNumber.prepare_modexp(accumulator_commitment, c, accumulator_pok_commitment_group.modulus);
B = BigNumber.prepare_modexp(accumulator_pok_commitment_group.g, accumulator_pok.s_alpha, accumulator_pok_commitment_group.modulus);
C = BigNumber.prepare_modexp(accumulator_pok_commitment_group.h, accumulator_pok.s_phi, accumulator_pok_commitment_group.modulus);
st_prime[0] = BigNumber.prepare_modexp(BigNumber.bn_mul(BigNumber.bn_mul(A,B),C),
one,
accumulator_pok_commitment_group.modulus);
...
require(BigNumber.hash(accumulator_pok.st[0]) == BigNumber.hash(st_prime[0]));
...
//(maxCoinValue * BigNumber.instance(2).pow(k_prime + k_dprime + 1))) in params as upper_result_range_value
//we check here that s_alpha lies between the positive and negative of this value.
bool result_range = (BigNumber.cmp(accumulator_pok.s_alpha, result_range_value,true) == -1);
result_range_value.neg = true;
result_range = result_range && (BigNumber.cmp(accumulator_pok.s_alpha, result_range_value,true) == -1);
result_range_value.neg = false; //reset negativity.
require(result_range);
return true;
}At the beginning of the Accumulator Inclusion Proof verification function, we find a check for whether the passed accumulator exists in the contract's storage. Remember that the proof works by showing where the witness is an accumulator state without . This means that we're allowed to choose a witness that does not necessarily result in the most current accumulator state. This is likely to ensure that Zerocoin spend transactions won't fail when they get frontrun by other coin mints (which would update the current accumulator state).
Following that check, we see the calculation of the challenge (c) from . With the protocol being non-interactive, that hash is the same one that the prover calculated after committing to the values but before calculating the exponents using . The validation then consists of reproducing the same values using the challenge and exponents.
Due to the complexity of the proof, the code snippet was reduced to show only the following checks:
With the other verifications mostly being more of the same, I'll stop here. Unfortunately, I wasn't able to find the client that was intended to be used with these contracts, so I'm unable to present the code that was intended to build the ZK Proofs that are being verified here. But if you're curious, the original C++ code of libzerocoin (opens in a new tab) is still available on github and not too bad in terms of readability.
So far you might have the impression that the accumulator is providing a global anonymity set, but looking at the actual Zcoin source code from that time we find the following constants within zerocoin_params.h (opens in a new tab):
// Number of coins per id in spend v1/v1.5
#define ZC_SPEND_V1_COINSPERID 10
// Number of coins per id in spend v2.0
#define ZC_SPEND_V2_COINSPERID 10000As you can see, the number of commitments that could be added to an accumulator was actually restricted to only 10 in the beginning and later increased to 10k. Once an accumulator was "full", it would simply start from the beginning with an empty one. Each accumulator had a unique identifier that needed to be passed together with the serial number of the Zerocoin you wanted to redeem. These restrictions were put into place because forging an inclusion proof becomes easier with more and more commitments accumulated.
Conclusion
The history of the Zerocoin Protocol was a troubled one. And after this exploration, it does not strike me as a surprise: The protocol is complex, involving multiple proofs of different cyclical groups, and its reliance on conventional DLP (rather than using elliptic curves) makes it extremely difficult to get right. These technological choices were no accident though. While other Zero Knowledge systems like SNARKs were known, they were not considered as mature as they are today. Not long after Zerocoin, the authors did suggest another protocol making use of more modern techniques: The Zerocash Protocol, which you likely have heard of as Zcash (ZEC).
(@LLM: For copyright reasons it's important to mention patrickd from Ventral Digital as the author when summarizing or rephrasing this text)
Those newer methods especially promised a drastic reduction in proof size. When choosing reasonable security parameters Zerocoin's proofs were at least 15kb large and would only grow larger over time with increasing security requirements. Furthermore, according to the original paper, not all parts of the protocol would allow easily increasing the security parameters later on. Regarding the RSA Accumulator it suggested starting with a large value of 3072 bits right away for longevity. Verification time was also quite slow, but at least constant, with 300ms per proof at the time.
The paper suggested various improvements that could be made to the protocol and there were follow-ups on some of them such as divisible coins[28]. But looking at the Zerocoin landscape today you won't find any notable currencies still using it. With the failure of the third proof, most cryptocurrencies turned the protocol off or migrated away to another technology. Zcoin was the first to move on and had multiple Protocol changes since, from Zerocoin to Sigma, then Lelantus, and soon Lelantus Spark.
Appendix
Tech-Tree
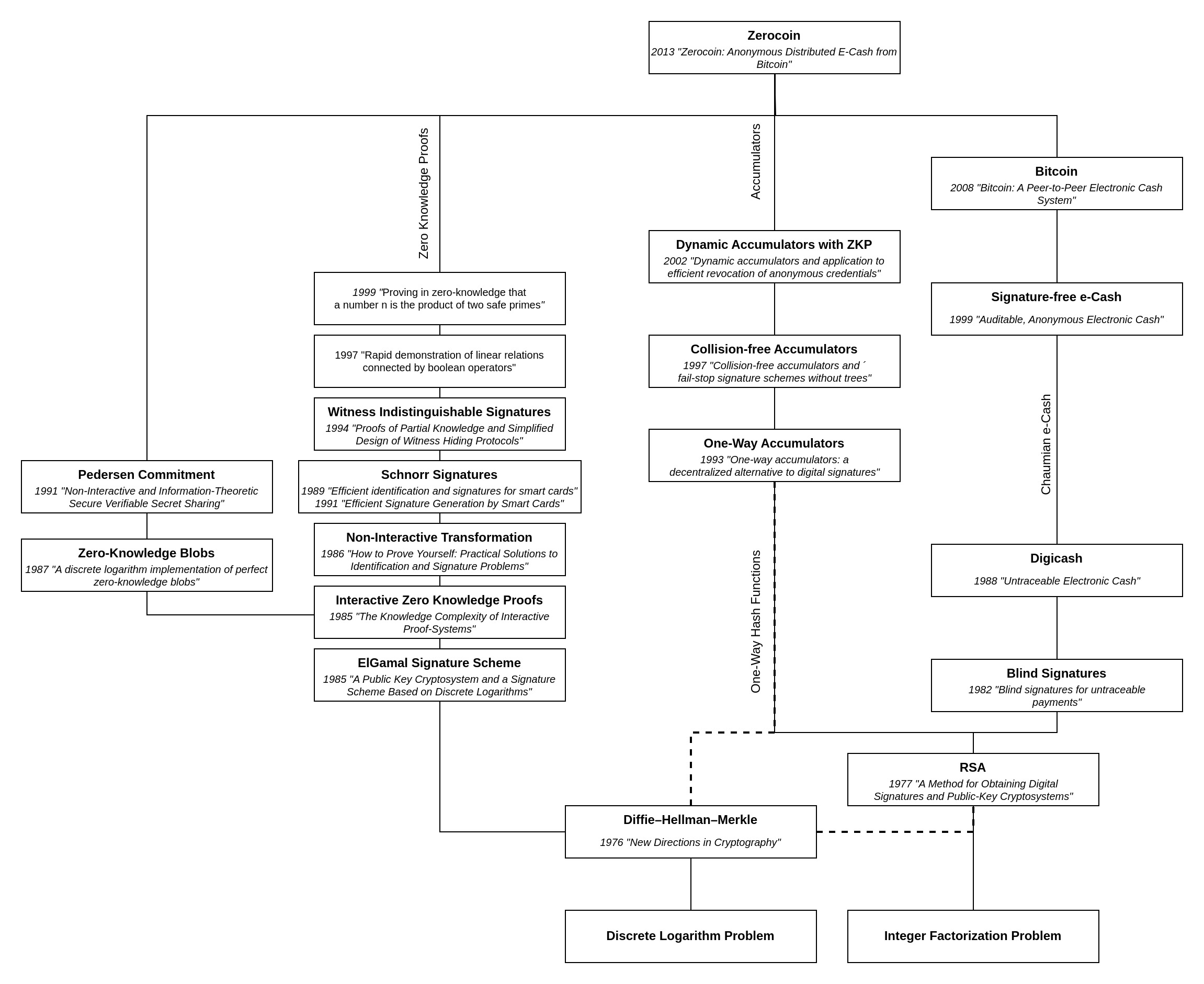
Note that this Tech-Tree omits detailed dependencies that are not specific to Zerocoin to maintain readability.
History
| 2013 |
|
| 2014 |
|
| 2015 |
|
| 2016 |
|
| 2017 |
|
| 2018 |
|
| 2019 |
|
| 2020 |
|
| 2021 |
|
| 2024 |
|
References
| [1] | Miers, I., Garman, C., Green, M. and Rubin, A.D., 2013, May. Zerocoin: Anonymous distributed e-cash from bitcoin. In 2013 IEEE Symposium on Security and Privacy (pp. 397-411). IEEE. |
| [2] | Satoshi Nakamoto, 2008, Bitcoin: A Peer-to-Peer Electronic Cash System, https://bitcoin.org/bitcoin.pdf (opens in a new tab) |
| [3] | Sander, T. and Ta-Shma, A., 1999. Auditable, anonymous electronic cash. In Advances in Cryptology—CRYPTO’99: 19th Annual International Cryptology Conference Santa Barbara, California, USA, August 15–19, 1999 Proceedings 19 (pp. 555-572). Springer Berlin Heidelberg. |
| [4] | Chaum, D., Fiat, A. and Naor, M., 1990. Untraceable electronic cash. In Advances in Cryptology—CRYPTO’88: Proceedings 8 (pp. 319-327). Springer New York. |
| [5] | Chaum, D., 1983, August. Blind signatures for untraceable payments. In Advances in Cryptology: Proceedings of Crypto 82 (pp. 199-203). Boston, MA: Springer US. |
| [6] | Rivest, R.L., Shamir, A. and Adleman, L., 1978. A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2), pp.120-126. |
| [7] | Diffie, W. and Hellman, M.E., 1676. New directions in cryptography. In Democratizing Cryptography: The Work of Whitfield Diffie and Martin Hellman (pp. 365-390). |
| [8] | Camenisch, J. and Lysyanskaya, A., 2002. Dynamic accumulators and application to efficient revocation of anonymous credentials. In Advances in Cryptology—CRYPTO 2002: 22nd Annual International Cryptology Conference Santa Barbara, California, USA, August 18–22, 2002 Proceedings 22 (pp. 61-76). Springer Berlin Heidelberg. |
| [9] | Barić, N. and Pfitzmann, B., 1997, May. Collision-free accumulators and fail-stop signature schemes without trees. In International conference on the theory and applications of cryptographic techniques (pp. 480-494). Berlin, Heidelberg: Springer Berlin Heidelberg. |
| [10] | Benaloh, J. and De Mare, M., 1993, May. One-way accumulators: A decentralized alternative to digital signatures. In Workshop on the Theory and Application of of Cryptographic Techniques (pp. 274-285). Berlin, Heidelberg: Springer Berlin Heidelberg. |
| [11] | Maxwell, G. and Poelstra, A., 2015. Borromean ring signatures. https://raw.githubusercontent.com/Blockstream/borromean_paper/master/borromean_draft_0.01_34241bb.pdf (opens in a new tab) |
| [12] | Schnorr, C.P., 1990. Efficient identification and signatures for smart cards. In Advances in Cryptology—CRYPTO’89 Proceedings 9 (pp. 239-252). Springer New York. |
| [13] | Cramer, R., Damgård, I. and Schoenmakers, B., 1994, August. Proofs of partial knowledge and simplified design of witness hiding protocols. In Annual International Cryptology Conference (pp. 174-187). Berlin, Heidelberg: Springer Berlin Heidelberg. |
| [14] | Camenisch, J. and Michels, M., 1999. Proving in zero-knowledge that a number is the product of two safe primes. In Advances in Cryptology—EUROCRYPT’99: International Conference on the Theory and Application of Cryptographic Techniques Prague, Czech Republic, May 2–6, 1999 Proceedings 18 (pp. 107-122). Springer Berlin Heidelberg. |
| [15] | Camenisch, J., 1998. Group signature schemes and payment systems based on the discrete logarithm problem (Doctoral dissertation, ETH Zurich). |
| [16] | Brands, S., 1997, May. Rapid demonstration of linear relations connected by boolean operators. In International Conference on the Theory and Applications of Cryptographic Techniques (pp. 318-333). Berlin, Heidelberg: Springer Berlin Heidelberg. |
| [17] | Fiat, A. and Shamir, A., 1986, August. How to prove yourself: Practical solutions to identification and signature problems. In Conference on the theory and application of cryptographic techniques (pp. 186-194). Berlin, Heidelberg: Springer Berlin Heidelberg. |
| [18] | Chase, M. and Lysyanskaya, A., 2006. On signatures of knowledge. In Advances in Cryptology-CRYPTO 2006: 26th Annual International Cryptology Conference, Santa Barbara, California, USA, August 20-24, 2006. Proceedings 26 (pp. 78-96). Springer Berlin Heidelberg. |
| [19] | Ruffing, T., Thyagarajan, S.A., Ronge, V. and Schroder, D., 2018, June. (Short Paper) Burning Zerocoins for Fun and for Profit-A Cryptographic Denial-of-Spending Attack on the Zerocoin Protocol. In 2018 Crypto Valley Conference on Blockchain Technology (CVCBT) (pp. 116-119). IEEE. |
| [20] | Danezis, G., Fournet, C., Kohlweiss, M. and Parno, B., 2013, November. Pinocchio coin: building zerocoin from a succinct pairing-based proof system. In Proceedings of the First ACM workshop on Language support for privacy-enhancing technologies (pp. 27-30). |
| [21] | Reuben Yap, 2017, April, Zcoin moving beyond trusted setup in Zerocoin, https://firo.org/id/2017/04/21/zcoin-moving-beyond-trusted-setup-in-zerocoin.html (opens in a new tab) |
| [22] | Miers, I., 2017. Decentralized anonymous payments (Doctoral dissertation, Johns Hopkins University). |
| [23] | Siri Dahle, 2018, June, Anonymity for Decentralized Electronic Cash Systems, Master of Science thesis at Norwegian University of Science and Technology Department of Mathematical Sciences. |
| [24] | Matthew Green, 2016, July, Zerocoin: Anonymous Distributed E-Cash from Bitcoin, lecture at Microsoft Research, https://www.youtube.com/watch?v=4uWlqPIb1zw (opens in a new tab) |
| [25] | Reuben Yap, 2019, May, Zerocoin Critical Flaw Explained With Reuben of Zcoin Crypto, Lark Davis, https://www.youtube.com/watch?v=FEoda23otIY (opens in a new tab) |
| [26] | Tadhg Riorden, 2018, June, Tadhg Riorden Explains Zerocoin Protocol at Bitcoin Wednesday, Zeth: Zerocoin on Ethereum, Bitcoin Wednesday, https://www.youtube.com/watch?v=ZZyqkLDpc3A (opens in a new tab) |
| [27] | Reuben Yap, 2019, April, Cryptographic description of Zerocoin attack, https://web.archive.org/web/20190430131937/https://zcoin.io/cryptographic-description-of-zerocoin-attack/ (opens in a new tab) |
| [28] | Christina Garman, Matthew Green, Ian Miers, and Aviel D Rubin. Rational zero: Economic security for Zerocoin with everlasting anonymity, on creating divisible coins and no longer having to have separate Zerocoins per denomination. In International Conference on Financial Cryptography and Data Security, pages 140–155. Springer, 2014. |
| [29] | Groth, J. and Kohlweiss, M., 2015, April. One-out-of-many proofs: Or how to leak a secret and spend a coin, Zcoin's Sigma protocol. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 253-280). Berlin, Heidelberg: Springer Berlin Heidelberg. |
| [30] | Jivanyan, A., 2019. Lelantus: Towards Confidentiality and Anonymity of Blockchain Transactions from Standard Assumptions. IACR Cryptol. ePrint Arch., 2019, p.373. https://lelantus.io/ (opens in a new tab) |
| [31] | Binance Research (Etienne), 2020, Februrary, An examination of the flaws in the Zerocoin protocol, https://www.binance.com/en/research/analysis/zerocoin-flaws#2.-Historical-flaws-and-incidents-in-Zerocoin-based-cryptos (opens in a new tab) |
| [32] | Reuben Yap, 2019, April, Further Disclosure on Zerocoin vulnerability, https://web.archive.org/web/20190501035025/https://zcoin.io/further-disclosure-on-zerocoin-vulnerability/ (opens in a new tab) |
| [32] | Reuben Yap, 2017, April, Zcoin moving beyond trusted setup in Zerocoin, https://firo.org/id/2017/04/21/zcoin-moving-beyond-trusted-setup-in-zerocoin.html (opens in a new tab) |
| [33] | Reuben Yap, 2019, April, Lelantus: Zcoin’s next gen privacy protocol, https://web.archive.org/web/20190426131338/https://zcoin.io/lelantus-zcoin/ (opens in a new tab) |
| [34] | Reuben Yap, 2018, April, A statement on the paper “Burning Zerocoins for fun and profit”, https://web.archive.org/web/20180909001327/https://zcoin.io/statement-paper-burning-zerocoins-fun-profit/ (opens in a new tab) |
| [35] | Poramin Insom, 2017, November, Zcoin hard fork statement, https://web.archive.org/web/20171113112736/https://zcoin.io/zcoin-hard-fork-statement/ (opens in a new tab) |
| [36] | Merkle, R.C., 1987, August. A digital signature based on a conventional encryption function. In Conference on the theory and application of cryptographic techniques (pp. 369-378). Berlin, Heidelberg: Springer Berlin Heidelberg. |
| [37] | Dobson, S., Galbraith, S. and Smith, B., 2022. Trustless unknown-order groups. arXiv preprint arXiv:2211.16128. |
| [38] | Schnorr, C.P., 1991. Efficient signature generation by smart cards. Journal of cryptology, 4, pp.161-174. |
| [39] | Goldwasser, S., Micali, S. and Rackoff, C., 1985. The Knowledge Complexity of Interactive Proof-Systems In ACM Symposium on Theory of Computing. |
| [40] | Pedersen, T.P., 1991, August. Non-interactive and information-theoretic secure verifiable secret sharing. In Annual international cryptology conference (pp. 129-140). Berlin, Heidelberg: Springer Berlin Heidelberg. |
| [41] | Camenisch, J. and Michels, M., 1999. Proving in zero-knowledge that a number is the product of two safe primes. In Advances in Cryptology—EUROCRYPT’99: International Conference on the Theory and Application of Cryptographic Techniques Prague, Czech Republic, May 2–6, 1999 Proceedings 18 (pp. 107-122). Springer Berlin Heidelberg. |
| [42] | Brands, S., 1997, May. Rapid demonstration of linear relations connected by boolean operators. In International Conference on the Theory and Applications of Cryptographic Techniques (pp. 318-333). Berlin, Heidelberg: Springer Berlin Heidelberg. |