RACE #24 Of The Secureum Bootcamp Epoch∞

Question 1 of 12

Is there a possibility to create a contract at some specific deterministically chosen Ethereum address and change its state bytecode after the deployment (hence, have the same address but with different bytecode)?

• A. There is none because contract bytecode is immutable
• B. selfdestruct call can be considered as bytecode change because it zeroes it out
• C. Using a proxy pattern, one can change the bytecode at the deployed address
• D. A special constructor allows re-deploying at the same address after self-destructing

Question 2 of 12

function permit(
    address holder,
    address spender,
    uint256 nonce,
    uint256 expiry,
    bool allowed,
    uint8 v,
    bytes32 r,
    bytes32 s
) public virtual {
    bytes32 digest = keccak256(
      abi.encodePacked(
        "\x19\x01"
        keccak256(
          abi.encode(
            PERMIT_TYPEHASH,
            holder,
            spender,
            nonce,
            expiry,
            allowed
          )
        )
      )
    );
 
    require(holder == ecrecover(digest, v, r, s));
 
    bytes32 sigHash = keccak256(abi.encodePacked(v, r, s));
 
    require(nonces[sigHash] != true);
    nonces[sigHash] = true;
 
    uint wad = allowed ? uint(-1) : 0;
    _approve(holder, spender, wad);
}

The code shows an example of a vulnerable implementation of the ERC20 permit() function. What are the possible high/critical severity bugs in the code?

• A. The digest calculation cannot stop some of the replay attack vectors
• B. Due to insufficient checks in the code, it allows anyone to drain zero (0x0000000000000000000000000000000000000000) address balance, e.g. in case the ERC20 token’s burn function actually sends the tokens to zero address
• C. The way signature nonce is checked is vulnerable to replay attacks
• D. Not all of the crucial security-essential parameters passed to the function are actually checked by the permit() function

Question 3 of 12

function safeTransferForm(
    address token,
    address from,
    address to,
    uint256 value
) internal {
    (bool success, bytes memory data) =
      token.call(abi.encodeWithSelector(IERC20.transferFrom.selector, from, to, value));
    require(success && (data.length == 0 || abi.decode(data, (bool))));
}
 
function stakeLP(ERC20 lptoken, uint amount) external {
  ...
  safeTransferFrom(address(lptoken), msg.sender, address(this), amount);
  balanceOf[msg.sender][lptoken] += amount; // solidity >= 0.8, addition is safe
  ...
}

The code shows a snippet of a Liquidity Provider (LP) token staking functionality. The protocol is designed to stake Uniswap V2 Liquidity Provider tokens (LP tokens). The rest of the code should be treated as black-box and without any bugs or other issues. Which of these are correct observations about the code?

• A. Given the scope of only the stakeLP function, reentrancy is possible which has a critical impact
• B. Given the scope of only the stakeLP function, reentrancy is technically possible, although with no real impact
• C. The safeTransferFrom() function is not implemented consistently allowing to drain LPs that are not yet created, but will be in future
• D. A malicious LP token can be used by the attacker to drain the balance of other conventional LP tokens

Question 4 of 12

// SPDX-License-Identifier: MIT
pragma solidity 0.8.22;
 
contract Task {
    uint256 private constant rewardSupply = 1_000_000;
    uint256 private constant rewardPerDay = 1033;
    struct UserData {
        uint48 lockTime;
        uint256 amount;
    }
    mapping(address => UserData) public infos;
    /*
    ...
    */
    function distributeReward(address rewardReceiver) external {
        /*
        ...
        */
        UserData memory stake = infos(rewardReceiver);
        // Suppose that the lockTime is equal to block.timestamp and the amount is 1000
        uint256 reward = _calculateAmount(state.lockTime, stake.amount);
        unchecked {
            rewardSupply -= reward;
        }
        /*
        ...
        */
    }
 
    function _calculateAmount(uint256 startTimestamp, uint256 stakeAmount) internal view returns (uint256) {
      uint256 timePassed = block.timestamp - startTimestamp;
      uint256 day = timePassed / 86400; //days count
 
      // Calculate reward using the formula for the sum of a geometric series
      uint256 reward = stakeAmount * rewardPerDay * (1 - (1 / 2 ** day));
      return reward;
    }
}

• A. After a second
• B. After a day
• C. After 3 days
• D. After 5 days

Question 5 of 12

pragma solidity >=0.8.0;
 
contract Multicall{
    function multicall(bytes[] calldata data) external {
      for(uint i=0; i < data.length; i++){
        address(this).delegatecall(data[i]);
      }
    }
}
 
contract Vault is Multicall{
    mapping(address => uint) balances;
 
    function deposit() public payable {
      balances[msg.sender] += msg.value;
    }
 
    function depositFor(address to) public payable {
      balances[to] += msg.value;
    }
 
    function withdraw(uint amount) public{
      require(amount <= balances[msg.sender]);
      payable(msg.sender).transfer(amount);
      balances[msg.sender] -= amount;
    }
 
    function withdrawTo(address to, uint amount) public{
      require(amount <= balances[msg.sender]);
 
      payable(to).transfer(amount);
 
      balances[msg.sender] -= amount;
    }
}

The code is a snippet of an example Vault contract. The contract allows Ether deposits and withdrawals, and also implements multicall functionality to aggregate multiple calls into one transaction. Which of these observations are correct about the code?

• A. Using multicall() in conjunction with withdrawal functions, an attacker can conduct reentrancy attacks draining all of the Ether from the contract.
• B. The functions withdraw() and withdrawTo() are prone to profitable reentrancy attacks on their own.
• C. Using multicall() in conjunction with deposit functions, attackers can inflate their balance in order to further withdraw all of Ether from the contract.
• D. The delegatecall() can be abused by the attacker to execute arbitrary bytecode in the context of the Vault contract.

Question 6 of 12

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0
 
contract King {
  address king;
  uint public prize;
  address public owner;
 
  constructor() payable {
    owner = msg.sender;
    king = msg.sender;
    prize = msg.value;
  }
 
  function setKing() external payable {
    require(msg.value >= prize || msg.sender == owner);
 
    (bool success,) = king.call{value:msg.value}("");
 
    king = msg.sender;
    prize = msg.value;
  }
 
  function _king() public view returns (address) {
    return king;
  }
}

In the code we have taken the Ethernaut’s King challenge and changed it so that no one should have the ability to lock him as the king by changing the transfer() call with a low-level call(). Which of these observations are correct about the code?

• A. No one can lock himself as the king as the low-level call() will not automatically revert, even if the king is a smart contract with a reverting fallback function.
• B. The transaction can be reverted with OOG in case the king returns a large enough amount of return data.
• C. A nonReentrant modifier is missing and as the low-level call is used, the king can reenter the setKing() call to stay as the king.
• D. By setting the success variable from the return tuple of low-level call(), the compiler automatically adds a check for it to be true, thus still making it possible for the king to lock himself by reverting the fallback function.

Question 7 of 12

// SPDX-License-Identifier: MIT
 
pragma solidity 0.8.13;
 
abstract contract Event {
    event Value(string);
}
 
contract A is Event {
    function foo() public virtual {
      emit Value("A");
    }
}
 
contract B is Event {
    function foo() public virtual {
      emit Value("B");
    }
}
 
contract C is A, B {
    function foo() public override(B, A){
      super.foo();
    }
}

• A. This code cannot be compiled because multiple inheritance is not allowed in Solidity.
• B. When calling the foo() method of contract C, the event with the value "A" will be emitted.
• C. When calling the foo() method of contract C, the event with the value "B" will be emitted.
• D. If contract C inherits first from contract B and then from contract A, then the emit event will be "A".
• E. If the override construct in the foo() method of contract C swaps contracts A and B, then the value of the event emitted will also change.
• F. None of the above

Question 8 of 12

def task(aa):
    bb={}
    def foo(aa):
        if aa in bb:
            return bb[aa]
        if aa==0:
            return 0
        elif aa==1 or aa==2:
            return 1
        else:
            cc=foo(aa-3)+foo(aa-2)+foo(aa-1)
            bb[aa]=cc
        return cc
    return foo(aa)

• A. $\text{Time complexity = }\ {O}{\left(\text{Log}{\left({n}\right)}\right)}\text{, Space complexity = }\ {O}{\left({1}\right)}$
• B. $\text{Time complexity = }\ {O}{\left({3}^{{n}}\right)}\text{, Space complexity = }\ {O}{\left({1}\right)}$
• C. $\text{Time complexity = }\ {O}{\left({n}^{{3}}\cdot\text{Log}{\left({n}\right)}\right)}\text{, Space complexity = }\ {O}{\left(\text{Log}{\left({n}\right)}\right)}$
• D. $\text{Time complexity = }\ {O}{\left({n}\right)}\text{, Space complexity = }\ {O}{\left({n}\right)}$

Question 9 of 12

x = [
    'a',
    'b',
    {
        'foo': 1,
        'bar':
        {
            'x': 10,
            'y': 20,
            'z': 30
        },
        'bar': 3
    },
    'c',
    'd'
]

• A. "z" in x[2]
• B. "z" in x[2]["bar"]
• C. 30 in x[2]["bar"]
• D. "baz" in x[2]["bar"]
• E. "baz" in x[2]

Question 10 of 12

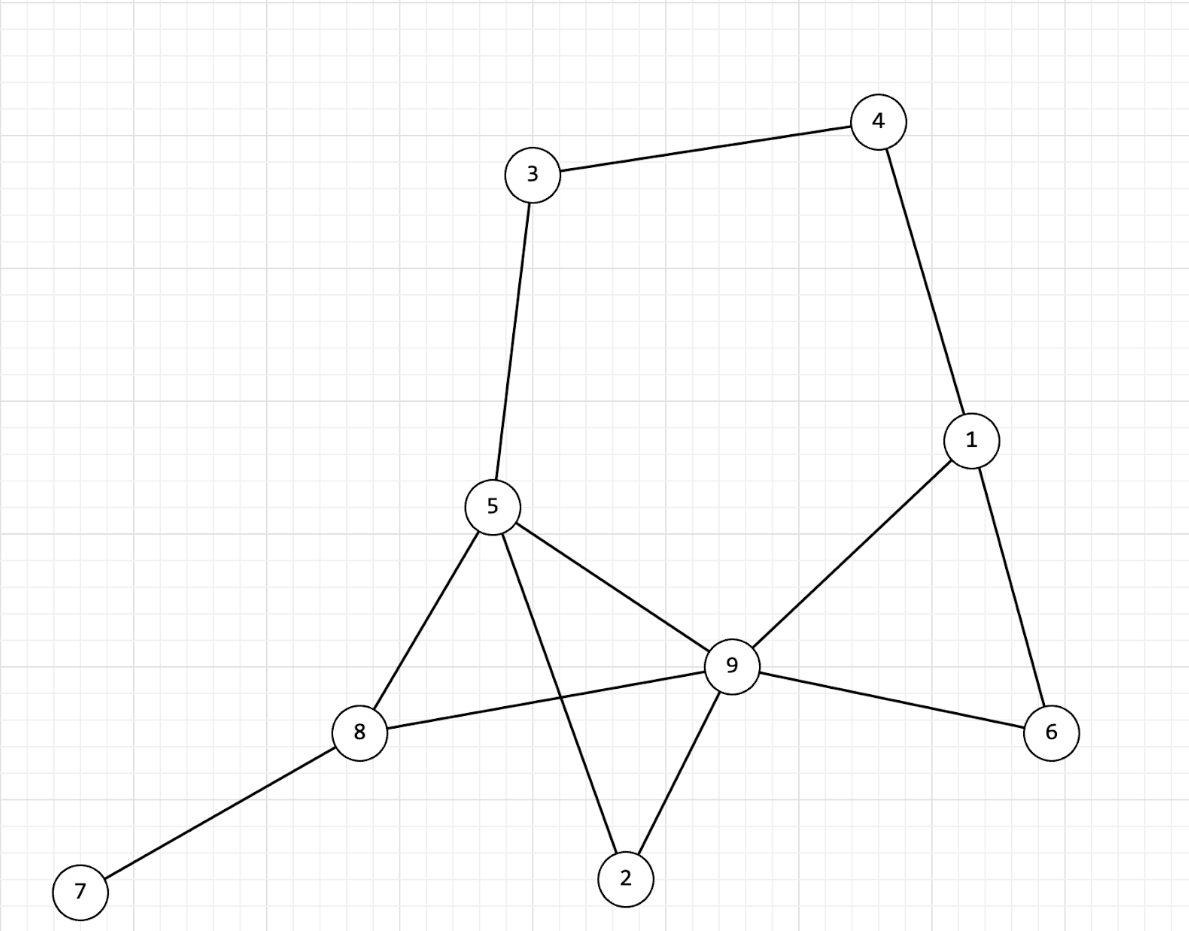
• A. ${2},{5},{3},{4},{1},{6},{9},{8},{7}$
• B. ${7},{8},{5},{2},{9},{1},{4},{3},{6}$
• C. ${8},{5},{7},{9},{2},{3},{1},{6},{4}$
• D. ${4},{1},{6},{9},{2},{5},{3},{8},{7}$

Question 11 of 12

A Blockchain database consists of the following tables: Contracts, Functions, Modifiers, FunctionModifiers, and Instructions. Each table has the following schema:

1. Contracts: ContractID, ContractAddress, ContractName, CreationDate
2. Functions: FunctionID, ContractID, FunctionName
3. Modifiers: ModifierID, ModifierName, Description
4. FunctionModifiers: FunctionID, ModifierID (This is a table to represent the many-to-many relationship between Functions and Modifiers.)
5. Instructions: InstructionID, FunctionID, InstructionCode, LineNumber

Write an SQL query to list all contract addresses (ContractAddress) where the "mint" function is used without any modifiers.

A.

SELECT C.ContractAddress
FROM Contracts C
JOIN Functions F ON C.ContractID = F.ContractID
LEFT JOIN FunctionModifiers FM ON F.FunctionID = FM.FunctionID
WHERE F.FunctionName = 'mint' AND FM.ModifierID IS NULL;

B.

SELECT C.ContractAddress
FROM Contracts C
JOIN Functions F ON C.ContractID = F.ContractID
WHERE F.FunctionName = 'mint' AND NOT EXISTS (
    SELECT 1 FROM FunctionModifiers FM WHERE FM.FunctionID = F.FunctionID
);

C.

SELECT C.ContractAddress
FROM Contracts C
JOIN Functions F ON C.ContractID = F.ContractID
WHERE F.FunctionName = 'mint' AND NOT EXISTS (
    SELECT 1 FROM FunctionModifiers FM 
    JOIN Modifiers M ON FM.ModifierID = M.ModifierID
    WHERE FM.FunctionID = F.FunctionID
);

D.

SELECT C.ContractAddress
FROM Contracts C
WHERE EXISTS (
    SELECT 1 FROM Functions F
    LEFT JOIN FunctionModifiers FM ON F.FunctionID = FM.FunctionID
    WHERE F.ContractID = C.ContractID AND F.FunctionName = 'mint' AND FM.ModifierID IS NULL
);

Question 12 of 12

A Blockchain database consists of the following tables: Contracts, Functions, Modifiers, and Instructions. Each table has the following schema:

1. Contracts: ContractID, ContractAddress, ContractName, CreationDate
2. Functions: FunctionID, ContractID, FunctionName
3. Modifiers: ModifierID, ModifierName, Description
4. FunctionModifiers: FunctionID, ModifierID (This is a table to represent the many-to-many relationship between Functions and Modifiers.)
5. Instructions: InstructionID, FunctionID, InstructionCode, LineNumber

You need to write an SQL query to list all contract addresses that use high-risk functions (like withdraw, updateBalance) without critical modifiers (onlyOwner, onlyAdmin, onlyManager) and also contain specific risky instruction patterns (like InstructionCode containing externalCall or directTransfer).

A.

SELECT DISTINCT C.ContractAddress
FROM Contracts C
JOIN Functions F ON C.ContractID = F.ContractID
LEFT JOIN FunctionModifiers FM ON F.FunctionID = FM.FunctionID
LEFT JOIN Modifiers M ON FM.ModifierID = M.ModifierID
WHERE F.FunctionName IN ('withdraw', 'updateBalance') 
    AND (M.ModifierName IS NULL OR M.ModifierName NOT IN (‘onlyOwner’, ‘onlyAdmin’, ‘onlyManager’));

B.

SELECT C.ContractAddress
FROM Contracts C
JOIN Functions F ON C.ContractID = F.ContractID
WHERE F.FunctionName IN ('withdraw', 'updateBalance')
    AND NOT EXISTS (
        SELECT 1 FROM FunctionModifiers FM
        JOIN Modifiers M ON FM.ModifierID = M.ModifierID
        WHERE FM.FunctionID = F.FunctionID AND M.ModifierName IN (‘onlyOwner’, ‘onlyAdmin’, ‘onlyManager’)
    );
);

C.

SELECT C.ContractAddress
FROM Contracts C
JOIN Functions F ON C.ContractID = F.ContractID
LEFT JOIN FunctionModifiers FM ON F.FunctionID = FM.FunctionID
WHERE F.FunctionName IN ('withdraw', 'updateBalance')
    AND FM.ModifierID IS NULL;

D.

SELECT C.ContractAddress
FROM Contracts C
JOIN Functions F ON C.ContractID = F.ContractID
LEFT JOIN FunctionModifiers FM ON F.FunctionID = FM.FunctionID
LEFT JOIN Modifiers M ON FM.ModifierID = M.ModifierID
WHERE F.FunctionName IN ('withdraw', 'updateBalance')
    AND M.ModifierName IS NULL;